Primer on symplecticity

Primer on symplecticity#

Symplectic condition#

Hamiltonian equation in matrix form#

For a N-dimensional Hamiltonian system (\(\mathbf{x}^N, \mathbf{p}^N\)), the N sets of Hamiltonian equation reads:

(1)#\[\begin{align} \frac{dx_i}{dt}&=\frac{\partial H}{\partial p_i}\\ \frac{dp_i}{dt}&=-\frac{\partial H}{\partial x_i} \end{align}\]

Let’s write a column vector \(X=(x_1, p_1, x_2,p_2,\cdots,x_N,p_n)\), the Hamiltonian can be written as:

(2)#\[\begin{align} \frac{d}{dt}X & \equiv S_N \frac{\partial H}{\partial X} = \left(\begin{array}{cccc} S_{2} & 0 & \cdots & 0\\ 0 & S_{2} & \cdots & 0\\ \vdots & \vdots & \ddots & 0\\ 0 & 0 & 0 & S_{2} \end{array}\right) \frac{\partial H}{\partial X} \end{align}\]

where \(S_1\) is the matrix for one dimension space:

(3)#\[\begin{align} S_2 = \left(\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right) \end{align}\]

Properties of S matrix#

We found that the following facts about \(S\) matrix

  • Determinant: \(\left|S\right|=1\)

  • Inverse: \(S^{-1}=-S \text{ or } S^2 = -I\)

  • The transpose: \(S^T=-S\)

For arbitrary 2 by 2 matrix \(A\) we may prove that:

(4)#\[\begin{equation} A^TS_2A=AS_2A^T= \left(\begin{array}{cc} 0 & \det A\\ -\det A & 0 \end{array}\right)=S_2\det A \end{equation}\]

Or we may define a new matrix \(\bar{A}=-S_2A^{T}S_2\) and yield:

(5)#\[\begin{equation} \bar{A}A=A\bar{A} = I\det{A} \end{equation}\]

Symplectic condition#

For a map from location \(s_0\) to \(s_1=s_0+s\), we have:

(6)#\[\begin{align} X\left(s_1\right)=M X\left(s_0\right) \end{align}\]

M is a matrix and the components is defined as:

(7)#\[\begin{align} M_{ij}=\frac{\partial X_i\left(s_1\right)}{ \partial X_j\left(s_0\right)} \end{align}\]

If \(M_{ij}\) are not functions of \(X\), the map represents a linear map. Otherwise \(M\) is a non-linear map. Regardless of the linearity, the condition that map \(M\) need to follow due to the system is a Hamiltonian system is called symplectic condition. We just explored the condition in 1-D case. In N-D system, from the Map definition:

(8)#\[\begin{align} X\left(s_1\right)=M X\left(s_0\right) \end{align}\]

We take the derivative of the \(i^{th}\) row of \(X(s_1)\) with respect to \(s\):

(9)#\[\begin{align} \frac{dX_i\left(s_1\right)}{ds} &=\frac{\partial X_i\left(s_1\right)}{\partial X_j\left(s_0\right)}\frac{dX_j\left(s_0\right)}{ds}\nonumber\\ &=M_{ij}S_{jk}\frac{\partial H}{\partial X_k\left(s_0\right)}\nonumber\\ &=M_{ij}S_{jk}\frac{\partial H}{\partial X_l\left(s_1\right)}\frac{\partial X_l\left(s_1\right)}{\partial X_k\left(s_0\right)}\nonumber\\ &=M_{ij}S_{jk}M_{kl}^T\frac{\partial H}{\partial X_l\left(s_1\right)} \end{align}\]

We know that

(10)#\[\begin{equation} \frac{dX_i\left(s_1\right)}{ds}=S_{il}\frac{\partial H}{\partial X_l\left(s_1\right)} \end{equation}\]

Therefore we have

(11)#\[\begin{align} MSM^T=S \end{align}\]

Using the property of \(S\), we have the usual form:

(12)#\[\begin{align} M^TSM=S %%\label{eq:symplectic_form} \end{align}\]

The equation (12) is referred as symplectic condition of a transfer map (not limited to matrix).

Properties of symplectic map#

The properties of the symplectic map:

  • If \(M\) is symplectic, so does \(M^T\) and \(M^{-1}\).

  • If \(M\) and \(N\) are symplectic, so does \(MN\).

  • The determinant of symplectic map is 1.

Properties of symplectic matrix#

The symplectic matrix has the following properties from the symplectic condition:

  • If \(\lambda\) is an eigenvalue of a symplectic matrix \(M\), so does \(1/\lambda\).

  • Every sympletic matrix has the inverse matrix: \(M^{-1}=-SM^{T}S\)

Block matrix for 2-D system#

Consider a 4-D phase space transfer map:

(13)#\[\begin{equation} \left(\begin{array}{cc} A & B\\ C & D \end{array}\right) \end{equation}\]

The transfer map has to satisfy the symplectic condition, both \(M^TSM=S\) and \(MSM^T=S\). For the first condition:

(14)#\[\begin{align} \left(\begin{array}{cc} A^T & C^T\\ B^T & D^T \end{array}\right) \left(\begin{array}{cc} S_2 & 0\\ 0 & S_2 \end{array}\right) \left(\begin{array}{cc} A & B\\ C & D \end{array}\right)&= \left(\begin{array}{cc} S_2 & 0\\ 0 & S_2 \end{array}\right) \end{align}\]
Hide code cell content 
import sympy 
sympy.init_printing(use_unicode=True)
a=sympy.MatrixSymbol('A', 2,2)
b=sympy.MatrixSymbol('B', 2,2)
c=sympy.MatrixSymbol('C', 2,2)
d=sympy.MatrixSymbol('D', 2,2)
s_2=sympy.MatrixSymbol('S_2', 2,2)
zero=sympy.ZeroMatrix(2,2)
M=sympy.BlockMatrix([[a,b],[c,d]])
ss=sympy.BlockMatrix([[s_2,zero],[zero,s_2]])
sympy.block_collapse(M.T*ss*M)
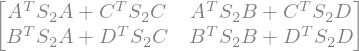
../_images/e42767328f226f702a10e516d675bd8fd6cfb21615d973429328a5c0562efa69.png
(15)#\[\begin{align} \left(\begin{matrix}A^{T} S_{2} A + C^{T} S_{2} C & A^{T} S_{2} B + C^{T} S_{2} D\\ B^{T} S_{2} A + D^{T} S_{2} C & B^{T} S_{2} B + D^{T} S_{2} D\end{matrix}\right)&= \left(\begin{array}{cc} S_2 & 0\\ 0 & S_2 \end{array}\right) \end{align}\]

Therefore the following relation satisfy:

(16)#\[\begin{split}\begin{align} A^{T} S_{2} A + C^{T} S_{2} C&=B^{T} S_{2} B + D^{T} S_{2} D=S_2 \\ A^{T} S_{2} B + C^{T} S_{2} D&=B^{T} S_{2} A + D^{T} S_{2} C=0 %%\label{Mmatzero} \end{align}\end{split}\]

Change \(M\) to \(M^T\), we have

(17)#\[\begin{split}\begin{align} A S_{2} A^{T} + B S_{2} B^{T}&=C S_{2} C^{T} + D S_{2} D^{T}=S_2 \\ A S_{2} C^{T} + B S_{2} D^{T}&=C S_{2} A^{T} + D S_{2} B^{T}=0 %%\label{Mtmatzero} \end{align}\end{split}\]

From the general property of 2-by-2 matrix \(A\):

(18)#\[\begin{align} A^TS_2A=AS_2A^T= \left(\begin{array}{cc} 0 & \det A\\ -\det A & 0 \end{array}\right) \end{align}\]

From the first set equations in (16) and (17), we know that:

(19)#\[\begin{split}\begin{align} \det A + \det C=\det D + \det B &=1\\ \det D + \det C=\det A + \det B &=1 \end{align}\end{split}\]

Or it can be re-written as:

(20)#\[\begin{align} \det A = \det D &\equiv a\\ \det B = \det C &\equiv b\\ a+b&=1 \end{align}\]

And from second set equations in (16) and (17), we have

(21)#\[\begin{split}\begin{align} \bar{A}B+\bar{C}D=\bar{B}A+\bar{D}C=0\\ A\bar{C}+B\bar{D}=C\bar{A} + D\bar{B}=0 \end{align}\end{split}\]

Note

It is worthwhile to note that, the symplectic condition for 4-D matrix (Eq. (19) and (21)) seems to have 9 equations on the coordinates. However, the actual constrains for 4-D are only 6.

The inverse of a blocked 4-by-4 matrix is simply:

(22)#\[\begin{align} M^{-1}&= \left(\begin{array}{cc} A & B\\ C & D \end{array}\right)^{-1}=-SM^TS \\ &=-\left(\begin{array}{cc} S_{1} & 0\\ 0 & S_{1} \end{array}\right) \left(\begin{array}{cc} A^T & C^T\\ B^T & D^T \end{array}\right) \left(\begin{array}{cc} S_{1} & 0\\ 0 & S_{1} \end{array}\right)\\ &=\left(\begin{array}{cc} \bar{A} & \bar{C}\\ \bar{B} & \bar{D} \end{array}\right) \end{align}\]

Here is a useful example. If we are exploring \(x\)-\(z\) or \(y\)-\(z\) phase space, the matrix \(U\) usually has the form below for DC magnets:

(23)#\[\begin{align} B= \left(\begin{array}{cc} \begin{array}{c} 0\\ 0 \end{array} & d=\left(\begin{array}{c} d_{1}\\ d_{2} \end{array}\right)\end{array}\right) \end{align}\]

Then

(24)#\[\begin{align} \det A = \det D &=1\\ \det B = \det C &=0 \end{align}\]

And from

(25)#\[\begin{align} \bar{B}A+\bar{D}C=0 \end{align}\]

We have

(26)#\[\begin{align} C=-D\bar{B}A \end{align}\]

Block matrix for 3-D system#

Consider a 6-D phase space transfer map:

(27)#\[\begin{equation} \left(\begin{array}{c} x\\ p_{x}\\ y\\ p_{y}\\ z\\ \delta \end{array}\right)_{2}=\left(\begin{array}{cc} M_{1} & C_1 & U_1\\ C_2 & M_{2} & U_2 \\ V_1 & V_{2} & M_3 \\ \end{array}\right)\left(\begin{array}{c} x\\ p_{x}\\ y\\ p_{y}\\ z\\ \delta \end{array}\right)_{1} \end{equation}\]
Hide code cell content 
import sympy 
sympy.init_printing(use_unicode=True)
m1=sympy.MatrixSymbol('M_1', 2,2)
m2=sympy.MatrixSymbol('M_2', 2,2)
m3=sympy.MatrixSymbol('M_3', 2,2)
u1=sympy.MatrixSymbol('U_1', 2,2)
u2=sympy.MatrixSymbol('U_2', 2,2)
c1=sympy.MatrixSymbol('C_1', 2,2)
v1=sympy.MatrixSymbol('V_1', 2,2)
v2=sympy.MatrixSymbol('V_2', 2,2)
c2=sympy.MatrixSymbol('C_2', 2,2)

s_2=sympy.MatrixSymbol('S_2', 2,2)
#s_2=sympy.Matrix([[0,1],[-1,0]])
zero=sympy.ZeroMatrix(2,2)
M=sympy.BlockMatrix([[m1,c1,u1],[c2,m2,u2],[v1,v2,m3]])
ss=sympy.BlockMatrix([[s_2,zero,zero],[zero,s_2,zero],[zero,zero,s_2]])
sympy.block_collapse(M*ss*M.T)
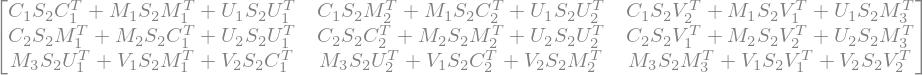
../_images/a4dc568adfe1101e09362cd3c00db02b6e60379c502d14db9d6eaeee52736ff9.png

Therefore, we can get the relation of the determinant of each block:

(28)#\[\begin{align} \det M_1 + \det C_1 + \det U_1 =1 \\ \det C_2 + \det M_2 + \det U_2 =1 \\ \det M_3 + \det V_1 + \det V_2 =1 \\ \end{align}\]

and

(29)#\[\begin{align} \det M_1 + \det C_2 + \det V_1 =1 \\ \det C_1 + \det M_2 + \det V_2 =1 \\ \det U_1 + \det U_2 + \det M_3 =1 \\ \end{align}\]

From the off diagonal blocks we have:

(30)#\[\begin{align} \bar{C}_2 M_2 + \bar{M}_1 C_1 + \bar{V}_1 V_2 &= 0 \\ \bar{C}_2 U_2 + \bar{M}_1 U_1 + \bar{V}_1 M_3 &= 0 \\ \bar{C}_1 U_1 + \bar{M}_2 U_2 + \bar{V}_2 M_3 &= 0 \\ C_1 \bar{M}_2 + M_1 \bar{C}_2 + U_1 \bar{U}_2 &= 0 \\ C_1 \bar{V}_2 + M_1 \bar{V}_1 + U_1 \bar{M}_3 &= 0 \\ C_2 \bar{V}_1 + M_2 \bar{V}_2 + U_2 \bar{M}_3 &= 0 \end{align}\]