Case Study: FODO Cell

9. Case Study: FODO Cell#

We will use FODO cell, with thin length Quadrupoles and small angle approximation for dipoles to illustrate various concepts of transverse dynamics.

Hide code cell source 
import matplotlib.pyplot as plt
%matplotlib ipympl
import numpy as np
import sympy
sympy.init_printing(use_unicode=True)
plt.rcParams.update({'font.size': 16})

9.1. Transfer Matrix of FODO cell#

FODO cell is a type of widely used cell of magnets. It consist of only two quadrupoles and two dipoles or simply drifts between quads. To make a symmetric cell, we use the following sequence:

\[\frac{1}{2}\text{QF}-\text{O}-\text{QD}-\text{O}-\frac{1}{2}\text{QF}\]

We use the following approximation:

  • Small bending angle approximation: the transfer matrix for a dipole reduces to a drift space, the space between quads are same, which is \(L_1\)

  • Short quadrupole approximation, so that the quad can be modeled by its focusing length \(f\)

  • Focusing length and defocusing length are same.

Then the matrix is

(9.1)#\[\begin{equation} M_{FODO}= \left(\begin{array}{cc} 1 & 0\\ -\frac{1}{2f} & 1 \end{array}\right) \left(\begin{array}{cc} 1 & L_1\\ 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & 0\\ \frac{1}{f} & 1 \end{array}\right) \left(\begin{array}{cc} 1 & L_1\\ 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & 0\\ -\frac{1}{2f} & 1 \end{array}\right) \end{equation}\]
Hide code cell source 
l,f,ff,fd,a=sympy.symbols(r"L_1,f,f_F,f_D,\alpha")
def mat_q(f):
    return sympy.Matrix([[1,0],[1/f,1]])
def mat_d(d):
    return sympy.Matrix([[1,d],[0,1]])
mat_fodo=sympy.simplify(mat_q(-2*ff)*mat_d(l)*mat_q(fd)*mat_d(l)*mat_q(-2*ff))
mat_fodo.subs(fd, ff)
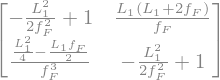
../../_images/172e3a5d3cf870568fefbb802788f6f5ecd59887efd795f560e4503f180c299c.png

The transfer matrix to/from the mid-point of the focusing quad is

(9.2)#\[\begin{equation} M_{FODO}= \left(\begin{matrix}- \frac{L_{1}^{2}}{2 f^{2}} + 1 & \frac{L_{1}}{f} \left(L_{1} + 2 f\right)\\\frac{L_{1}}{4 f^{3}} \left(L_{1} - 2 f\right) & - \frac{L_{1}^{2}}{2 f^{2}} + 1\end{matrix}\right) \end{equation}\]

The determinant of the matrix is always 1. The trace of the FODO cell is \(2- \frac{L_{1}^{2}}{ f^{2}} \).

The starting point can be choose arbitrarily. If we use the midpoint of the defocusing quad:

Hide code cell source 
mat_fodo_2=sympy.simplify(mat_q(2*f)*mat_d(l)*mat_q(-f)*mat_d(l)*mat_q(2*f))
mat_fodo_2
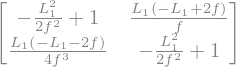
../../_images/2eb6af6f63835de7b79c5fa8f75c4cf8e76085c0a363fb45221a514c8b20938e.png

The transfer matrix becomes:

(9.3)#\[\begin{equation} M_{FODO,midQD}= \left(\begin{matrix}- \frac{L_{1}^{2}}{2 f^{2}} + 1 & \frac{L_{1}}{f} \left(- L_{1} + 2 f\right)\\- \frac{L_{1}}{4 f^{3}} \left(L_{1} + 2 f\right) & - \frac{L_{1}^{2}}{2 f^{2}} + 1\end{matrix}\right) \end{equation}\]

The trace remain unchanged.

Hide code cell source 
mat_fodo_3=sympy.simplify(mat_d(0)*mat_q(f)*mat_d(l)*mat_q(-f)*mat_d(l))
mat_fodo_3
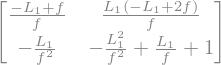
../../_images/9e20c52b3cbcdbe6a4813f2cb4cbd2b64a9558608cbbd1234f1ddce9c51fabea.png

If we set the starting point right after the focusing quadrupole, the matrix becomes

(9.4)#\[\begin{equation} M_{FODO,afterQF}= \left(\begin{matrix}\frac{1}{f} \left(- L_{1} + f\right) & \frac{L_{1}}{f} \left(- L_{1} + 2 f\right)\\- \frac{L_{1}}{f^{2}} & - \frac{L_{1}^{2}}{f^{2}} + \frac{L_{1}}{f} + 1\end{matrix}\right) \end{equation}\]

Again the trace remain unchanged. That is a natural result since trace of the product of matrices is an invariant under cyclic permutation.

9.2. FODO cell in repeating structure#

To use the FODO cell many time in a repeating structure, the trace has to be larger than \(-2\). Therefore:

\[- \frac{L_{1}^{2}}{2 f^{2}} + 1 > -1 \]

which reduces to:

\[L_1<2f\]

Then we can get the optics parameters of the one-turn matrix:

\[\begin{split} M=\left(\begin{array}{cc} \cos\Phi+\alpha\sin\Phi & \beta\sin\Phi\\ -\gamma\sin\Phi & \cos\Phi-\alpha\sin\Phi \end{array}\right) \end{split}\]

Then the betatron phase advance can be calculated from:

(9.5)#\[\begin{equation} \cos{\Phi}=\frac{1}{2}\operatorname{tr}(M)=1-\frac{L_1^2}{2f^2} \end{equation}\]

or

(9.6)#\[\begin{equation} \sin{\frac{\Phi}{2}}=\frac{L_1}{2f} \end{equation}\]

The trace is an invariant under changing the starting piont, so does the phase advance.

The optical function can be calculated at different locations by:

(9.7)#\[\begin{align} \beta &= \frac{M_{12}}{\sin\Phi}\\ \alpha &= \frac{M_{11}-M_{22}}{2\sin\Phi} \end{align}\]

At the middle point of the QD or QF we have:

(9.8)#\[\begin{align} \beta_{F/D} &= \frac{2L_1\left(1\pm\sin(\Phi/2)\right)}{\sin\Phi}\\ \alpha &= 0 \end{align}\]

Right after the focusing quad, we have:

(9.9)#\[\begin{align} \beta &= \frac{2L_1\left(1-\sin(\Phi/2)\right)}{\sin\Phi}\\ \alpha &= \frac{L_1}{f}\frac{\sin(\Phi/2)-1}{\sin\Phi} \end{align}\]

9.3. Dispersion in FODO cells#

Let’s consider the FODO cells with small bending angle approximation, starting from the mid point of the focusing quad. The extended \(3\times 3\) matrix \(\mathcal{M}\) gives

(9.10)#\[\begin{equation} \mathcal{M}_{FODO}= \left(\begin{array}{cc} 1 & 0 & 0\\ -\frac{1}{2f} & 1 & 0\\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & L_1 & L_1 \theta/2\\ 0 & 1 & \theta \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & 0 & 0\\ \frac{1}{f} & 1 & 0\\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & L_1 & L_1 \theta/2\\ 0 & 1 & \theta \\ 0 & 0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & 0 & 0\\ -\frac{1}{2f} & 1 & 0\\ 0 & 0 & 1 \end{array}\right) \end{equation}\]
Hide code cell source 
t=sympy.symbols("\\theta")
def matd_q(f):
    return sympy.Matrix([[1,0,0],[1/f,1,0],[0,0,1]])
def matd_d(d, ang):
    return sympy.Matrix([[1,d,d*ang/2],[0,1,ang],[0,0,1]])
mat_fodo=sympy.simplify(matd_q(-2*f)*matd_d(l,t)*matd_q(f)*matd_d(l,t)*matd_q(-2*f))
mat_fodo
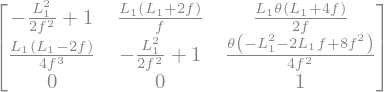
../../_images/8da4f85a43972ef9260cac32d2841eed7e8cf8403604c4519580c04d9820f93e.png

The matrix \(\mathcal{M}\) of FODO cell gives

(9.11)#\[\begin{equation} \mathcal{M}_{FODO}= \left(\begin{matrix}- \frac{L_{1}^{2}}{2 f^{2}} + 1 & \frac{L_{1}}{f} \left(L_{1} + 2 f\right) & \frac{L_{1} \theta}{2 f} \left(L_{1} + 4 f\right)\\\frac{L_{1}}{4 f^{3}} \left(L_{1} - 2 f\right) & - \frac{L_{1}^{2}}{2 f^{2}} + 1 & \frac{\theta}{4 f^{2}} \left(- L_{1}^{2} - 2 L_{1} f + 8 f^{2}\right)\\0 & 0 & 1\end{matrix}\right) \end{equation}\]
Hide code cell source 
s=sympy.symbols('\sin(\phi/2)')
sympy.simplify(sympy.Inverse(sympy.eye(2)-mat_fodo[:2,:2])*mat_fodo[:2,2]).subs(f, l/2/s)

<>:1: SyntaxWarning: invalid escape sequence '\s'
<>:1: SyntaxWarning: invalid escape sequence '\s'
/var/folders/6f/_6jt88pn2gl5zsg16g5zt1z40000gq/T/ipykernel_2533/1931797471.py:1: SyntaxWarning: invalid escape sequence '\s'
  s=sympy.symbols('\sin(\phi/2)')
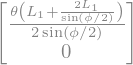
../../_images/f4e54274da3c72eb607cd53ca6f4d369b9b6df68c5aed62fa37e5989f8410755.png

The dispersion function in periodical boundary condition gives:

(9.12)#\[\begin{equation} \left(\begin{array}{c} D\\ D' \end{array}\right) _{midQF}= \left(\begin{matrix}\frac{L_1\theta}{2 \sin(\Phi/2)} \left(1 + \frac{2}{\sin(\Phi/2)}\right)\\0\end{matrix}\right) \end{equation}\]

One can easily get the dispersion function at the middle point of the defocusing quad as:

(9.13)#\[\begin{equation} \left(\begin{array}{c} D\\ D' \end{array}\right)_{midQD} = \left(\begin{matrix}\frac{L_1\theta}{2 \sin(\Phi/2)} \left(-1 + \frac{2}{\sin(\Phi/2)}\right)\\0\end{matrix}\right) \end{equation}\]

With the choice of the phase advance, the maximum and minimum of the beta function and dispersion functions can be optimized base on the requirements.

Hide code cell source 
epsilon=0.2
phi=np.linspace(epsilon,np.pi-epsilon,100)
beta_max=2*(1+np.sin(phi/2))/np.sin(phi)
eta_max=(np.sin(phi/2)+2)/2/np.sin(phi/2)/np.sin(phi/2)
beta_min=2*(1-np.sin(phi/2))/np.sin(phi)
eta_min=(-np.sin(phi/2)+2)/2/np.sin(phi/2)/np.sin(phi/2)
fig,ax=plt.subplots()
ax_m=ax.twinx()
ax.set_xlabel("Phase advance [rad]")
ax.set_ylabel(r"$\beta$ [in unit of $L$]")
ax_m.set_ylabel(r"$D$ [in unit of $L\theta$]")
ax.set_ylim(0,10)
ax.set_xlim(0,np.pi)
ax_m.set_ylim(-0,10)
l1=ax.plot(phi,beta_max,c='b',label=r'$\beta_{max}$')
l2=ax.plot(phi,beta_min,c='c',label=r'$\beta_{min}$')
l3=ax_m.plot(phi,eta_max, c='y', label=r'$D_{max}$')
l4=ax_m.plot(phi,eta_min, c='r', label=r'$D_{min}$')
lns = l1+l2+l3+l4
labs = [l.get_label() for l in lns]
ax.legend(lns,labs,loc='right')
ax.set_xticks(np.linspace(0,1,5,)*np.pi)
ax.set_xticklabels(["$0$", r"$\frac{1}{4}\pi$", r"$\frac{1}{2}\pi$",
                    r"$\frac{3}{4}\pi$", r"$\pi$",
                     ])

fig.tight_layout()

9.4. Chromaticity of FODO cell#

The natural chromaticity of this lattice has contributions from the two thin quadrupoles

(9.14)#\[\begin{align} C_x&=-\frac{1}{4\pi}\int\beta_x K_x ds \\ &=-\frac{1}{4\pi f}\left(\beta_{max} - \beta_{min}\right) \\ &=-\frac{\tan(\Phi/2)}{\pi} \\ &=-\frac{\tan(\Phi/2)}{\Phi/2} \nu_x \end{align}\]

9.5. \(\mathcal{H}\) function in FODO cell#

We have optics at the middle of QF and QD

(9.15)#\[\begin{align} \beta_{F/D} &= \frac{2L_1\left(1\pm\sin(\Phi/2)\right)}{\sin\Phi}\\ D_{F/D} &= \frac{L_1\theta}{2 \sin(\Phi/2)} \left( \pm 1 + \frac{2}{\sin(\Phi/2)}\right) \end{align}\]

Therefore the \(\mathcal{H}\) at these two location gives:

(9.16)#\[\begin{align} \mathcal{H}_{F/D} &= \frac{L\theta^2 \cos(\Phi/2)}{\sin^3(\Phi/2)\left(1\pm\sin(\Phi/2) \right)} \left(1\pm\frac{1}{2}\sin\frac{\Phi}{2}\right)^2 \end{align}\]

Let’s replace the integral with the average of the value at both end of the dipole.

(9.17)#\[\begin{align} \rho\frac{I_5}{I_2} &= \rho\frac{\oint\frac{\mathcal{H}}{\rho^3}ds}{\oint\frac{1}{\rho^2}ds} \\ &=\frac{1}{2}\left({\mathcal{H}_{F}+\mathcal{H}_{D}}\right) \\ &=\frac{\rho\theta^3 \cos(\Phi/2)}{2\sin^3(\Phi/2)} \left(\frac{\left(1+\frac{1}{2}\sin\frac{\Phi}{2}\right)^2}{\left(1+\sin(\Phi/2) \right)}+ \frac{\left(1-\frac{1}{2}\sin\frac{\Phi}{2}\right)^2}{\left(1-\sin(\Phi/2) \right)}\right) \\ &=\rho\theta^3\frac{ \cos(\Phi/2)}{\sin^3(\Phi/2)\cos(\Phi/2)}\left(1-\frac{3}{4}\sin^2\frac{\Phi}{2}\right) \end{align}\]

The maxmumum, minimum \(\mathcal{H}\) function and the approximated \(\mathcal{H}\) in dipoles are also functions of the phase advance of the FODO cell.

Hide code cell source 
epsilon=0.2
phi=np.linspace(epsilon,np.pi-epsilon,100)
beta_max=2*(1+np.sin(phi/2))/np.sin(phi)
eta_max=(np.sin(phi/2)+2)/2/np.sin(phi/2)/np.sin(phi/2)
beta_min=2*(1-np.sin(phi/2))/np.sin(phi)
eta_min=(np.sin(phi/2)-2)/2/np.sin(phi/2)/np.sin(phi/2)

H_min=eta_max*eta_max/beta_max
H_max=eta_min*eta_min/beta_min


    
loc=np.argmin(H_max+H_min)
print(phi[loc]/np.pi*180, (H_max+H_min)[loc]/2)
chrom=-np.tan(phi/2.0)/(phi/2.0)

fig,ax=plt.subplots()
ax_m=ax.twinx()
ax.set_xlabel("Phase advance [rad]")
ax.set_ylabel(r"$\mathcal{H}$ in unit of $\rho \theta^3$")
ax_m.set_ylabel(r"Specific chromaticity $\xi/\nu$")
ax.set_ylim(0,10)
ax.set_xlim(0,np.pi)
#ax_m.set_ylim(-10,10)
l1=ax.plot(phi,(H_max+H_min)/2.0, c='b', label=r'Average $\mathcal{H}$')
l2=ax.plot(phi,H_max,c='y',label=r'$\mathcal{H}_{max}$', alpha=0.4)
l3=ax.plot(phi,H_min,c='c',label=r'$\mathcal{H}_{min}$', alpha=0.4)
l4=ax_m.plot(phi,chrom, c='r', label=r'Chromaticity $\xi$')
lns = l1+l2+l3+l4
labs = [l.get_label() for l in lns]
ax.legend(lns,labs,loc=3)
ax.set_xticks(np.linspace(0,1,5,)*np.pi)
ax.set_xticklabels(["$0$", r"$\frac{1}{4}\pi$", r"$\frac{1}{2}\pi$",
                    r"$\frac{3}{4}\pi$", r"$\pi$",
                     ])
ax.axvline(x=phi[loc], ls='--', lw=.5)

labs = [l.get_label() for l in lns]
ax.legend(lns,labs,loc=3)
fig.tight_layout()

138.39385343374136 1.18777034003462